The harmonic oscillator states are nondegenerate. Therefore, we can apply nondegenerate to find the first-order correction to the
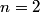 energy level due to the perturbation to the Hamiltonian. energy level due to the perturbation to the Hamiltonian.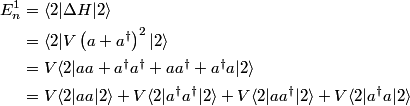 Both 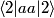 and and 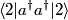 must equal must equal 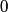 because of the orthognality of the eigenstates. Therefore, because of the orthognality of the eigenstates. Therefore,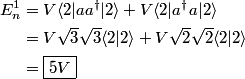 Therefore, answer (E) is correct. |